|
|
Abb. 1 |
|
|
Abb. 2 |
|
|
Abb. 3 |
|
|
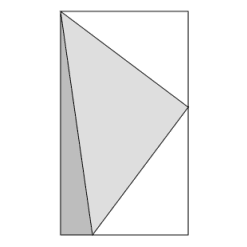
Abb. 4 |
|
|
Abb. 5 |
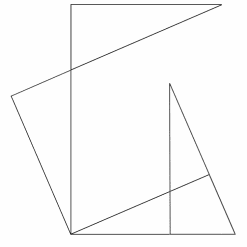
|
|
Abb. 6 |
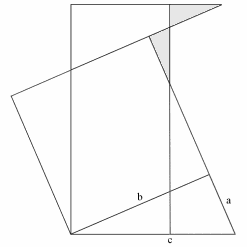
|
|
Abb. 7 |
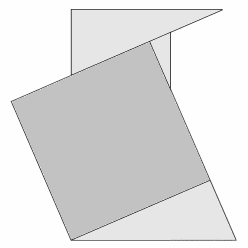
|
|
Abb. 8 |
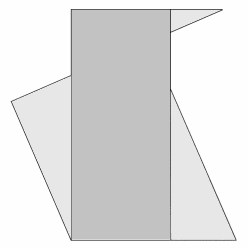
|
|
Abb. 9 |
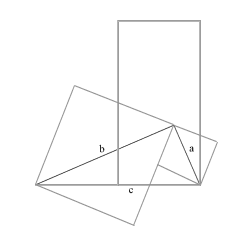
|
|
Abb. 10 |
|
|
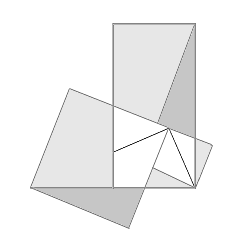
Abb. 11 |
Aufbau der Beweisfigur
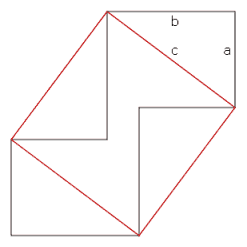
In Abb. 1 wurden vier kongruente, rechtwinklige Dreiecke mit den beiden Katheten a und b und der Hypotenuse c, teils außen, teils innen, an das (rote) Hypotenusenquadrat c2 angelegt. Dadurch entsteht im Hypotenusenquadrat ein (blitzförmiges) Sechseck.
Beweis
Dieses Sechseck ergibt zusammen mit den beiden rechtwinkligen Dreiecken links und rechts das Hypotenusenquadrat c2. Zusammen mit den beiden rechtwinkligen Dreiecken oben und unten ergibt das Sechseck das große schwarze Achteck, das somit den gleichen Flächeninhalt wie c2 haben muss. Das Achteck besteht aus zwei Quadraten mit der Kantenlänge a links unten und rechts oben und einem schmalen Rechteck mit der Breite (b - a) und der Höhe (b + a). Somit ist:
2a2 + (b - a)(b + a) = c2
2a2 + b2 - a2 = c2
a2 + b2 = c2
2. Beweis
Aufbau der Beweisfigur
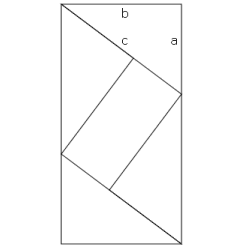
In Abb. 2 wurden vier kongruente, rechtwinklige Dreiecke so angeordnet, dass ein Rechteck mit den Kantenlängen b und (c + a) entsteht. Im Rechteck liegt eine Raute mit der Kantenlänge c. Innerhalb dieser Raute liegt wiederum ein Rechteck, diesmal mit den Kantenlängen (c - a) und b.
Beweis
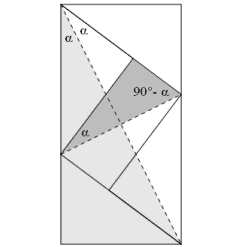
Es soll gezeicht werden, dass die beiden grauen Dreiecke aus Abb. 3 ähnlich sind. Dazu genügt es zu zeigen, dass die beiden kleineren der spitzen Winkel in den grauen Dreiecken gleich sind. Aus Abb. 3 isr ersichtlich, dass diese Winkel α gleich sind, da die Diagonalen einer Raute sich senkrecht schneiden und die Diagonalen die Winkel der Raute halbieren. Somit verhalten sich die Katheten der beiden grauen Dreiecke gleich:
b / (c + a) = (c - a) / b
b2 = (c - a)(c + a)
b2 = c2 - a2
a2 + b2 = c2
3. Beweis
Aufbau der Beweisfigur
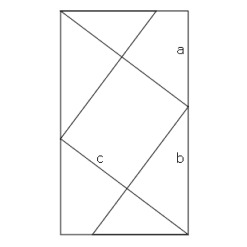
In Abb. 4 wurden vier kongruente, rechtwinklige Dreiecke so angeordnet, dass ein Rechteck mit den Kantenlängen b und (a + b) entsteht. In Abb. 5 sieht man, dass sich dieses Rechteck aus vier rechtwinkligen Dreiecken zusammensetzt, nämlich aus 2 Dreiecken mit den Katheten a und b, einem Dreieck mit den Katheten c und einem Dreieck mit den Katheten (b - a) und (b + a).
Beweis
das große Rechteck mit den Kantenlängen b und (a + b) hat den gleichen Flächeninhalt wie die Summe der vier rechtwinkligen Dreiecke:
b(a + b)½ab + ½ab + ½c2 + ½(b - a)(b + a)
ab + b2 = ab + ½c2 + ½b2 - ½a2
b2 = ½c2 + ½b2 - ½a2
½a2 + ½b2 = ½c2
a2 + b2 = c2
Kathetensatz
Die Figur aus Abb. 4 kann auch zum Beweis des Kathetensatzes b2 = cq herangezogen werden. Das Rechteck mit den Kantenlängen b und (a + b) ist nämlich auch zusammengesetzt aus zwei rechtwinkligen Dreiecken oben und unten mit den Katheten a und b und einem Parallelogramm mit den Seiten b und c und der zur Seite c gehörigen Höhe q. Dieses Parallelogramm hat somit den Flächeninhalt cq und es gilt:
b(a + b) = ½ab + ½ab + cq
ab + b2 = ab + cq
b2 = cq
4. Beweis
Aufbau der Beweisfigur
Zunächst werden vier kongruente rechtwinklige Dreiecke zu einer Figur wie in Abb. 6 angeordnet. Danach wird diese Figur so ergänzt, dass ein Quadrat und ein Rechteck enstehen (Abb. 7).
Beweis
Zunächst soll gezeigt werden, dass das Quadrat (aus Abb. 8) und das Rechteck (aus Abb. 9) den gleichen Flächeninhalt haben. Dazu muss gezeigt werden, dass die beiden grauen Dreiecke in Abb. 7 kongruent sind und somit den gleichen Flächeninhalt haben.
Die längere Kathete des unteren grauen Dreiecks hat die Länge (a + b) - c. Die längere Kathete des oberen grauen Dreiecks hat die Länge a - (c - b) = a - c + b. Diese beiden Katheten sind also gleich lang. Da außerdem an diesen beiden Katheten ein rechter Winkel anliegt und jeweils ein gleich großer Winkel gegenüber liegt (Scheitelwinkel), sind die beiden grauen Dreiecke kongruent (nach Kongruenzsatz WWS).
Wenn ich von der Gesamtfigur in Abb. 8 das obere und untere rechtwinklige Dreieck und das untere der beiden kleineren Dreiecke abziehe, bleibt das Quadrat b2 übrig.
Wenn ich von der gleichen Gesamtfigur in Abb. 9 das linke und rechte rechtwinklige Dreieck und das obere der beiden kleineren Dreiecke abziehe, bleibt das Rechteck (c - a)(c + a) übrig.
Da ich von der Gesamtfigur drei jeweils paarweise kongruente Dreiecke abgezogen habe, sind die beiden Figuren, die übrig bleiben, flächeninhaltsgleich. Somit ist:
b2 = (c - a)(c + a)
b2 = c2 - a2
a2 + b2 = c2
5. Beweis
In diesem Beweis soll die Gleichung ½a2 + ½b2 = ½c2 bewiesen werden.
Aufbau der Beweisfigur
Die Quadrate ½a2 und ½b2 werden so um die beiden Katheten a und b gezeichnet, dass a und b jeweils die Diagonalen der Quadrate bilden. Dadurch liegen die beiden Quadrate nebeneinander. Die Fläche ½c2 wird als Rechteck mit den beiden Seiten ½c und c über die Hypotenuse gezeichnet (Abb. 10).
Beweis
Um zu beweisen, dass ½a2 + ½b2 = ½c2 und somit a2 + b2 = c2, soll die Fläche ½a2 + ½b2 so zerlegt werden, dass die Teile das Rechteck ½c2 genau ausfüllen. Dazu muss gezeigt werden, dass die grauen Flächen aus Abb. 11 paarweise kongruent sind:
1. Die beiden kleinen grauen Dreiecke aus Abb. 11 sind kongruent (Kongruenzsatz WSW), weil
a) ... die beiden längeren Katheten jeweils gleichzeitig die Seite des kleineren Quadrates und somit gleich lang sind,
b) ... die beiden Winkel, die aneinander stoßen, durch eine Drehung um 90° aufeinander abgebildet werden können
c) ... und beide Dreiecke einen rechten Winkel haben.
2. Die beiden größeren dunkelgrauen Dreiecke sind kongruent (Kongruenzsatz WWS), weil
a) ... die beiden Hypotenusen so lang sind wie c minus der Hypotenuse der kleinen Dreiecke,
b) ... jeweils ein Winkel Scheitelwinkel zu einem Winkel der bereits kongruenten kleinen Dreiecke ist
c) ... und beide Dreiecke wiederum einen rechten Winkel haben.
3. Die beiden grauen Vierecke könnten durch Punktspiegelung aufeinander abgebildet werden. Alle Winkel sind paarweise gleich, denn die Vierecke habe je zwei gegenüberliegende rechte Winkel und ein weiterer Winkel liegt dem entsprechenden Winkel des anderen Vierecks als Scheitelwinkel gegenüber.
Jeweils eine Seite der Vierecke ist so lang wie die Seite des rößeren Quadrates bzw. wie die längere Kathete des rößeren grauen Dreiecks. Die nächste Seite, die dann gegen den Uhrzeigersinn folgt, ist so lang wie ½c.